Los últimos resultados de las Pruebas Aprender dieron cuenta de que solo el 14,2% de los alumnos de secundaria alcanzó un nivel Satisfactorio en la evaluación de competencias en matemática, un indicador que conforma una serie de resultados “considerablemente más bajos” en esta materia en comparación con Lengua, la otra asignatura en la que se basó el relevamiento.
La Evaluación Nacional Aprender se llevó a cabo el 24 de octubre del año pasado en 11.846 escuelas de todo el país, con 379.050 estudiantes de 5to y 6to año.
“En términos generales el 58% de los estudiantes alcanzan o superan el nivel satisfactorio en Lengua y un 14,2% en Matemática. Mientras que en Lengua se observa una mayor proporción de estudiantes alcanzando los niveles esperados, en Matemática los resultados son considerablemente más bajos, incluso en los sectores con mayores recursos y en el sector de gestión privada donde uno de cada cuatro alcanza este nivel”, indicó la Secretaría de Educación –dependiente del Ministerio de Capital Humano– en su informe oficial.
Esta situación, añadieron, “sugiere la existencia de desafíos persistentes en la enseñanza y el aprendizaje de esta área, que podrían estar vinculados a aspectos más profundos del funcionamiento del sistema educativo, más allá de las condiciones individuales o familiares”.
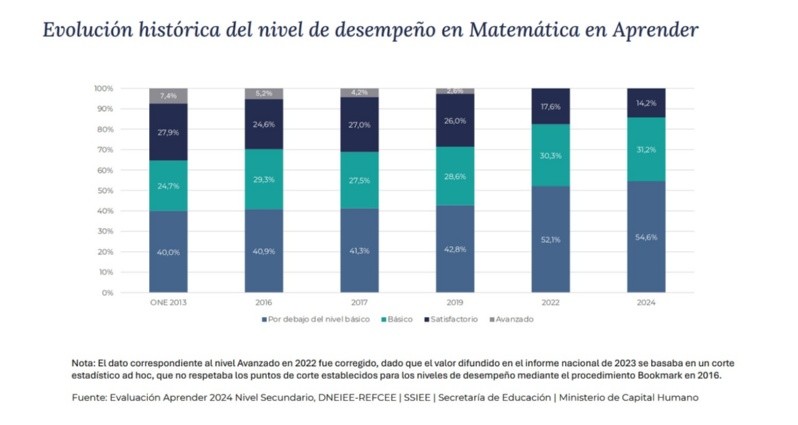
Concretamente en el caso de Matemática, desde Educación constataron que “el 85,8% de los estudiantes presentan desempeños Bajos o Debajo del básico” (31,2% se ubicó en nivel básico y 54,6% por debajo), por lo que solo el 14,2% restante alcanza el nivel Satisfactorio.
“Se verifica una disminución sostenida (a excepción de 2017) de la proporción de estudiantes con los niveles de desempeño más altos: de 35,3% en 2013 al 14% en 2024”, una caída de 21 puntos porcentuales, advirtieron.
Una muestra de las pruebas
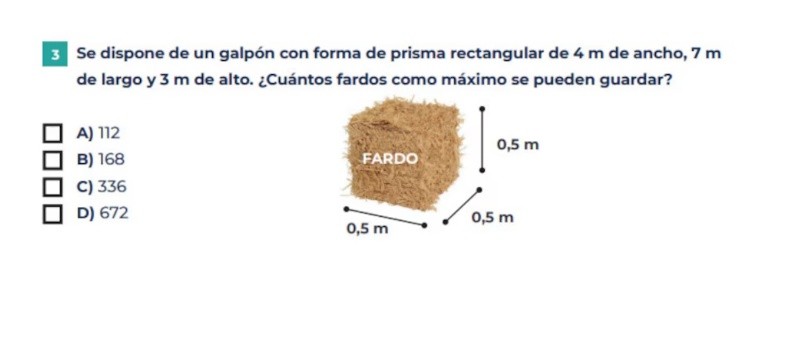
La evaluación presentó consignas habituales de la enseñanza secundaria, organizadas en áreas como funciones, álgebra, geometría, trigonometría y estadística. Según precisaron desde el área de educación, se trató de problemas aplicados a situaciones simples y reconocibles que requerían interpretar información, razonar con lógica y realizar cálculos básicos. En cada ítem de la prueba había cuatro respuestas posibles (A, B, C y D). La consigna de uno de los ejercicios pedía identificar uno o más intervalos que contienen las raíces de una función cuadrática, es decir, los puntos en los que una curva corta el eje horizontal. En este caso, la opción correcta fue elegida por el 30,6% de los estudiantes. Una proporción significativa de los estudiantes confundió las raíces con el vértice de la parábola –el punto donde la curva cambia de dirección–, lo que reveló dificultades para interpretar la relación entre los valores de una tabla y su representación gráfica. Otro ejercicio representaba la escena de una persona sentada frente a un escenario, y pedía calcular el ángulo desde el cual observaba una lámpara colgada del techo. Para resolverlo, se ofrecían distintas formas de relacionar la altura de la lámpara con la distancia al escenario. Las opciones correspondían a tres razones trigonométricas clásicas: seno, coseno y tangente. La clave era identificar cuál de esas razones se aplicaba correctamente a los datos del problema, algo que solo el 30% logró. Otra de las consignas, en este caso de las más sencillas, requiere resolver una situación que involucra el concepto de volumen del prisma. La dificultad corresponde al nivel Satisfactorio de la prueba. También se incluyó un problema relacionado con promedios, usando como ejemplo un conjunto de pelotitas de colores a las que se sumaban más unidades de un nuevo color. Los estudiantes debían calcular el nuevo promedio. Aunque se trataba de un ejercicio de nivel básico, más de la mitad no supo resolverlo. Mientras que algunos omitieron sumar los nuevos elementos, otros dividieron entre valores incorrectos, en tanto que muchos no distinguieron entre los datos a sumar y la cantidad de categorías. Para resolver otro de los ejercicios, los alumnos tenían que identificar la expresión algebraica de una función lineal dada por su gráfico. Esta consigna corresponde al nivel “Avanzado” de la prueba, al que no llegó ningún estudiante en todo el país. Según explica el Manual Aprender, los estudiantes que resuelven bien este ejercicio identifican en el gráfico la pendiente (-1) y la ordenada al origen (1) de la recta graficada. De esta manera son capaces de elegir la expresión algebraica de la recta graficada que es y = -x + 1 (la opción B).